Физика и реализация реально зрелищных анимаций может показаться очень сложной затеей, но на самом деле это не так. Эти алгоритмы могут быть очень простыми и могут производить реалистичное моделирование различных физических понятий, включая скорость, ускорение или гравитацию.

Итак, давайте посмотрим, как работают эти алгоритмы при реализации двумерного физического моделирования в JavaScript!

Равномерное и ускоренное движение

Давайте начнем с самого простого — перемещать объекты вокруг.
Если мы хотим просто равномерное движение, то мы можем использовать такой код:

function move(dt) {
    x += vx * dt;
    y += vy * dt;
}

В приведенном выше коде x и y — координаты объекта, например, эллипс, next vx и vy — скорости по горизонтальной и вертикальной оси соответственно, а dt (дельта времени) — это время между 2 тактами таймера, что в случае JavaScript есть 2 вызова на requestAnimationFrame.
Как пример — если бы мы хотели переместить объект, сидящий в (150, 50) и двигаясь на юго-запад, то у нас было бы следующее (движение после одиночного тика):

x = 150 += -1 * 0.1 -> 149.9
y =  50 +=  1 * 0.1 -> 50.1

Равномерное движение довольно скучно, поэтому давайте ускорим движение наших объектов:

function move(dt) {
    vx += ax * dt;
    vy += ay * dt;
    x += vx * dt;
    y += vy * dt;
}

В этом фрагменте кода мы добавили ax и ay, которые представляют ускорение по осям x и y соответственно. Мы используем ускорение для вычисления изменения скорости или скорости (vx / vy), которое мы затем используем для перемещения объектов, как раньше. Теперь, если мы скопируем предыдущий пример и добавим ускорение только по оси X (на запад), мы получим:

vx =  -1 += -1   * 0.1 ->  -1.1  // vx += ax * dt;
vy =   1 +=  0   * 0.1 ->   1    // vy += ay * dt;
 x = 150 += -1.1 * 0.1 -> 149.89 //  x += vx * dt;
 y =  50 +=  1   * 0.1 ->  50.1  //  y += vy * dt;

Сила тяжести

Теперь, когда мы можем перемещать объекты, как насчет перемещения объектов к другим объектам? Ну, это просто называется гравитацией. Что нам нужно добавить, чтобы реализовать это?

Перво-наперво, давайте вспомним несколько уравнений из средней школы, а именно уравнение силы:

F = m * a
a = F / m

Если мы теперь хотим расширить это на силу двух объектов, действующих друг на друга, мы получим:

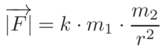
Это становится немного сложным (по крайней мере для меня), поэтому давайте разберемся с этим. В этом уравнении | F | величина силы, которая одинакова для обоих объектов, только в противоположном направлении. Эти объекты представлены их массой — m_1 и m_2. k здесь — гравитационная постоянная, а r — расстояние центров тяжести этих объектов. Если это все еще не имеет особого смысла, то вот картинка:

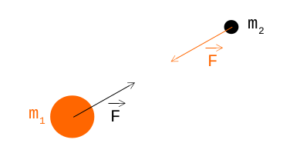
Если мы хотим создать некоторую визуализацию, мы получим более двух объектов, верно? Итак, что происходит, когда у нас больше объектов, действующих друг на друга?

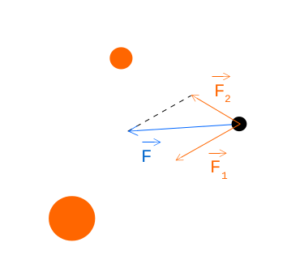
Глядя на картинку выше, мы можем видеть 2 оранжевых объекта, тянущих черный с силами F_1 и F_2, хотя нас интересует конечная сила F, которую мы можем вычислить так:

• Сначала мы рассчитываем силы F_1 и F_2, используя уравнения сверху

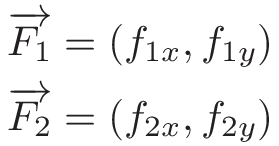
• Затем мы разбиваем его на векторы:

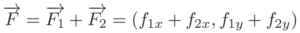
Хорошо, у нас есть все, что нам нужно, теперь, как будет выглядеть код? Я избавлю вас от всех шагов и просто покажу вам окончательный код с комментариями ?

function moveWithGravity(dt, o) {  // «o» относится к массиву объектов, которые мы перемещаем
    for (let o1 of o) {  // Нулевой аккумулятор сил для каждого объекта
        o1.fx = 0;
        o1.fy = 0;
    }
    for (let [i, o1] of o.entries()) {  // Для каждой пары объектов 
        for (let [j, o2] of o.entries()) {
            if (i < j) {  // To not do same pair twice
                let dx = o2.x - o1.x;  // Вычислить расстояние между центрами объектов
                let dy = o2.y - o1.y;
                let r = Math.sqrt(Math.pow(dx, 2) + Math.pow(dy, 2));
                if (r < 1) {  // Чтобы избежать деления на 0
                    r = 1;
                }
                // Вычислить силу для этой пары; к = 1000
                let f = (1000 * o1.m * o2.m) / Math.pow(r, 2);  
                let fx = f * dx / r;  // Разбейте его на составляющие
                let fy = f * dy / r;
                o1.fx += fx;  // Накопить за первый объект
                o1.fy += fy;
                o2.fx -= fx;  // И для второго объекта в противоположном направлении
                o2.fy -= fy;
            }
        }
    }
    for (let o1 of o) {  // для каждого обновления объекта ...
        let ax = o1.fx / o1.m;  // 
        let ay = o1.fy / o1.m;

        o1.vx += ax * dt;  // ...скорость
        o1.vy += ay * dt;

        o1.x += o1.vx * dt;  // ...позиция
        o1.y += o1.vy * dt;
    }
}

Столкновения

Когда объекты движутся, они также сталкиваются в некоторый момент. У нас есть два варианта разрешения коллизий — выталкивать объекты из коллизии или отскакивать, давайте сначала посмотрим на решение для толкания:

Прежде чем мы сможем разрешить конфликт, нам нужно сначала проверить, действительно ли сталкиваются 2 объекта:

class Collision {
    constructor(o1, o2, dx, dy, d) {
        this.o1 = o1;
        this.o2 = o2;

        this.dx = dx;
        this.dy = dy;
        this.d = d;
    }
}

function checkCollision(o1, o2) {
    let dx = o2.x - o1.x;
    let dy = o2.y - o1.y;
    let d = Math.sqrt(Math.pow(dx, 2) + Math.pow(dy, 2));
    if (d < o1.r + o2.r) {
        return  {
            collisionInfo: new Collision(o1, o2, dx, dy, d),
            collided: true
        }
    }
    return  {
        collisionInfo: null,
        collided: false
    }
}

Сначала мы объявляем класс Collision, который представляет 2 сталкивающихся объекта. В функции checkCollision мы сначала вычисляем x и y компоненты расстояний объектов, а затем вычисляем их фактическое расстояние d. Если сумма их радиусов меньше, чем их расстояние d, то они должны быть в столкновении, поэтому мы возвращаем новый объект Collision.

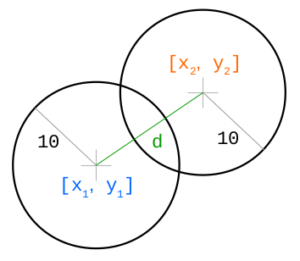
Теперь, чтобы разрешить их столкновение, нам нужно знать направление смещения и его величину:

n_x = d_x / d
n_y = d_y / d

s = r_1 + r_2 - d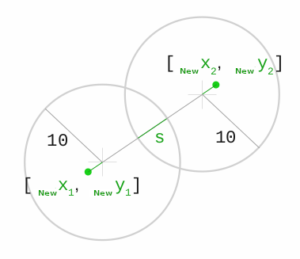

Итак, в коде JavaScript это будет:

function resolveCollision(info) {  // «информация» является объектом столкновения сверху
    let nx = info.dx /info.d;  // Вычислить собственные векторы
    let ny = info.dy /info.d;
    let s = info.o1.r + info.o2.r - info.d; // Вычислить глубину проникновения
    info.o1.x -= nx * s/2;  // Переместить первый объект на половину размера столкновения
    info.o1.y -= ny * s/2;
    info.o2.x += nx * s/2;  // Переместить другой объект на половину размера столкновения в противоположном направлении.
    info.o2.y += ny * s/2;
}

Столкновения при помощи силы

И последний кусок головоломки — разрешение столкновений путем подпрыгивания объектов. В этом случае лучше не использовать всю математику, так как это сделает статью вдвое длиннее, поэтому все, что я хочу вам сказать, это то, что нам нужно учитывать закон сохранения импульса и закон сохранения энергии, который помогает нам построить и решить следующее магическое уравнение:

k = -2 * ((o2.vx - o1.vx) * nx + (o2.vy - o1.vy) * ny) / (1/o1.m + 1/o2.m)

Как этот магический k помогает нам? Мы знаем направление, в котором будут двигаться объекты (мы можем вычислить это, используя собственные векторы, как раньше, с n_x и n_y), но мы не знаем, насколько это и есть k. Итак, вот как мы вычисляем вектор (z), который говорит нам, куда перемещать эти объекты:

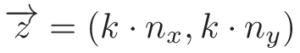
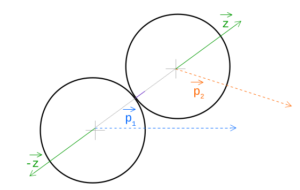
А теперь окончательный код:

function resolveCollisionWithBounce(info) {
    let nx = info.dx /info.d;
    let ny = info.dy /info.d;
    let s = info.o1.r + info.o2.r - info.d;
    info.o1.x -= nx * s/2;
    info.o1.y -= ny * s/2;
    info.o2.x += nx * s/2;
    info.o2.y += ny * s/2;

    let k = -2 * ((info.o2.vx - info.o1.vx) * nx + (info.o2.vy - info.o1.vy) * ny) / (1/info.o1.m + 1/info.o2.m);
    info.o1.vx -= k * nx / info.o1.m;
    info.o1.vy -= k * ny / info.o1.m;
    info.o2.vx += k * nx / info.o2.m;
    info.o2.vy += k * ny / info.o2.m;
}

Вывод

В этом посте много математики, но большая часть довольно проста, поэтому я надеюсь, что это помогло вам понять и ознакомиться с этими физическими понятиями.